Making a Strategy Game with Chess-like AI in Pico-8 - 3#: AI Design
I'm Ross. I'm a chemical engineer and I make tiny games in my spare time. I recently made a strategy game with Chess-like AI from scratch in Pico-8. In this series of posts I'll walk you through my design process and share what I learnt throughout.
AI Design
Now we come to the heart of the project: writing an AI that can play tafl.
With tafl being a niche strategy game, the history of engine development for the game is not well-documented. When it comes to tafl engines, OpenTafl seems to be the most prominent, however I found limited documentation explaining how this engine actually works. Additionally, as discussed in my previous posts, tafl lacks a standardised ruleset. There are many variations in capture mechanics, win conditions, and even board sizes across different versions of the game. This means that any tafl engine would need to be adapted to the specific ruleset it is playing with, making it difficult to rely on an all-purpose approach.
In contrast, there's a wealth of documentation readily available online explaining how a chess engine is programmed, dating all the way back to 1948, when Alan Turing, one of the pioneers of computer science, developed the first chess engine algorithm. Interestingly, Turing's algorithm had to be followed manually by hand since there was no computer capable of running it at the time!
Given the abundance of resources and the well-documented history of chess engine development, I decided to tackle this problem by writing my own chess engine and modifying it to play tafl.
Chess Engine Resources
On setting out to write my own chess engine, I knew I needed a solid understanding of how a chess engine functions.
Whilst the Chess Programming Wiki proved to be a useful resource due to the vast amount of information it hosts, for a high-level comprehensive overview of what goes into programming a chess engine, I found the following video by Sebastian Lague incredibly useful. I would recommend it as starting point for anyone who is looking to learn how to programme their own engine.
Once I had a high-level understanding of how a chess engine functions, I began reviewing the source code of various chess engines to gain a deeper understanding of their programming. Two engines in particular were especially helpful.
SecondChess proved to be an incredibly useful resource; it is a very basic chess engine written in C, with frequent and clear comments that enhance readability.
TSCP (Tom's Simple Chess Program) is another great resource, intended for people who want to learn about chess programming. It is written as a tutorial engine, with its source code designed to be very easy to understand. Despite it being written as a tutorial engine, however, I found it significantly harder to wrap my head around compared to the SecondChess engine. Fortunately, I didn't seem to be alone in this opinion, as I came across the following write up in which the TSCP engine has been further explained.
For the rest of this post, I'll walk you through the process of building my own chess engine and modifying it to play tafl in Pico 8.
Board Representation and Piece Movement
The first step in programming a strategy game involves deciding how to represent the game board, similar to the concept of board representation in chess engines. Before tackling the gameplay mechanics, we must first write a structure that can store all of the relevant details about the game’s current state.
There are different methods in which this can be accomplished, however newcomers to chess programming are encouraged to use a square centric approach. In this approach, each square on the board is represented by a unique integer number. As Ziege is a tile-based game played on a 7x7 board, we can apply a similar board representation, allocating sequential numbers to each square like so:
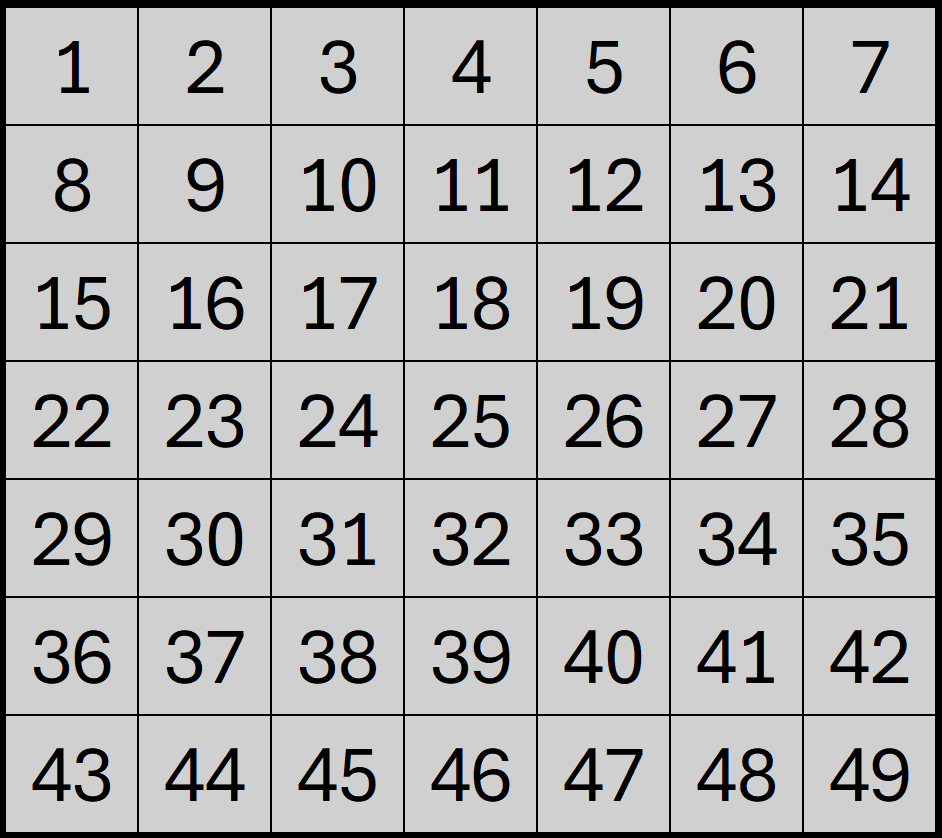
Structuring the board as a one-dimensional array is common in chess programs as it simplifies how the computer processes the game. Instead of thinking in terms of rows and columns, the board is treated as a single line of 64 squares (or 49 squares in our game's case) and a pieces position on the board is represented by one of these numbers.
Using a one-dimensional array representation of the board, moving pieces becomes a straightforward task of adding or subtracting a specific number from the piece's current position. For example, in Ziege, moving a piece one square forward or backward corresponds to adding or subtracting 7 (the size of one row in a 7x7 grid). Similarly, moving one square to the left or right means adding or subtracting 1. This approach eliminates the complexity of tracking row and column positions separately, simplifying how moves are handled.
You may be wondering, however, as we are not tracking row and column positions, how do we determine when a piece has left the board? To detect this, we can use a technique involving a larger board with a boundary of invalid squares surrounding the play area like so:

We use this bigger 9x9 board when moving pieces; any attempt to move pieces outside of the playable area results into the invalid squares is prevented. Piece movement for Ziege is therefore defined by the following movement array:
-- piece movement (up,right,down,left)
piece_movement = {-9, 1, 9, -1}
In Ziege, all pieces move like the rook in chess; in a straight line for as many empty squares as the player chooses. Pieces cannot hop over other pieces and cannot move diagonally.
For a given piece, we can therefore determine all of its available legal moves by iterating over each direction in the movement array and checking every square in that direction until we either encounter an occupied square or reach the edge of the board by adding the corresponding value from the piece_movement array repeatedly to the current position of the piece.
Capture Logic
One of the most notable differences between Ziege and chess is how captures are made. In chess, capturing an opponent’s piece is straightforward — any piece that moves onto a square occupied by an opponent’s piece captures the opposing piece. Ziege, however, has a different mechanic for captures. Pieces are not captured by moving onto their square. Instead, a piece is captured by flanking it on two opposite sides. For example, if an opponent's piece is trapped between two of your pieces, one on either side, it is captured and removed from the board.

Similar to how we determine all of a piece’s legal moves by iterating through each direction in the piece_movement array, we can apply a similar approach for captures. From the destination square of a piece's move, we look at the adjacent squares for an opponent's piece. If an opponent’s piece is found, we then check the square beyond it in the same direction to see if it contains one of our own pieces. If so, this move would result in the opponent’s piece being trapped between two of our pieces; we can then log this move as a successful capture.
How the AI Operates
The AI operates similarly to a traditional chess engine; using a Minimax algorithm.
To begin with, the engine generates a list of all the possible legal moves, simulates each one, and evaluates the resulting board positions. Each position is assigned a numerical score that reflects how favourable the engine perceives it to be. Selecting the best move seems straightforward; just choose the one with the highest score! However, sometimes a move might look promising at first glance, but it's no good if it leaves the player vulnerable to a strong counterattack!
To account for this we don't just evaluate the immediate board state; we also simulate the opponent’s potential responses. The score of the original move is then based on the least favourable outcome after the opponent's best response is considered.
The minmax algorithm is primarily made up of two key components: a search function and an evaluation function. These two components work together to analyse and choose the best moves to play in a game of chess.
Search Function
At the core of the Minimax algorithm is the search function, which explores the possible moves for both players and evaluates the resulting board positions. In Ziege, I implemented a recursive function (a function that calls itself) to simulate each move, alternating between the maximising player score (the AI) and the minimising player score (the human opponent).
The search function looks at all possible moves a given side can make, tries each one, and checks what the board would look like afterward. It then does the same for the opponent's moves, going back and forth until it reaches a set number of moves ahead (the desired search depth).
However, due to the shear number of possible moves that can be made in a given position, if we were to store every possible board state that we search we would very quickly run out of memory! We can overcome this problem, however, by instead evaluating every possible board state on a single instance of the board. Once we have made a move (or series of moves) on the board, we evaluate the resulting position and then take back that same series of moves so that we end up at our original board position.
To streamline this process, we can write two helper functions:
makemove(): Makes a move on the board and updates the board state to reflect it .takemove(): Reverts the board to its previous state after a move has been simulated.
Using these helper function, our final search function then looks akin to the following:
function _search (depth) {
if depth == 0 then
return evaluate_board()
end
local moves = generate_moves()
local bestscore = -32000
for move in all(moves) do
makemove(move)
local score = -search(depth-1)
takemove(move)
if score > bestscore then
bestscore = score
end
end
return bestscore
end
Board Evaluation
The evaluation function assigns a score to each board state, determining how favorable it is for the AI. This function is critical to the AI’s decision-making, as it influences which moves are determined to be best as a result of the search.
Similarly to a simple chess engine, we can based the evaluation on two primary factors:
- Material balance: The difference in the number of pieces for each side.
- Piece positioning: Encouraging strategic placement of pieces.
Starting with the material balance, the game pieces are assigned a material value. For Ziege, I went with the following point values:
- Infected pieces: 300 points
- Scientist pieces: 280 points
- Head Scientist piece: 10,000 points
In general, trading pieces often benefits the Scientists, as fewer pieces on the board results in more open lines that the Head Scientist can use to escape. By valuing the Infected pieces ever so slightly higher than the Scientist pieces, the AI will avoid trading pieces, unless the trade is beneficial for it (for example, if the trade removes a well-placed piece for a poorly-placed piece).
The Head Scientist piece is given a very large value; in doing so the AI will always prioritise capturing the head scientist piece if it can do so.
However, this is only useful if we are comparing positions with different amount of pieces. What if we want to compare two different positions with the same amount of pieces? For this we look at piece positioning.
Chess engines utilise piece square tables to change the value of a given piece depending on where it is located on the board. We can use piece square values similarly for Ziege. In a game of tafl, the attacking pieces aim to surround the defending pieces to prevent them from escaping. Therefore, for the Infected pieces, we can utilise the following piece square table to encourage the AI to form a chain of infected pieces around it opponents pieces:
piece_square_table_infected = [
-30, -10, 0, 30, 0, -10, -30,
-10, 20, 30, 20, 30, 20, -10,
0, 30, 10, 10, 10, 30, 0,
30, 20, 10, 0, 10, 20, 30,
0, 30, 10, 10, 10, 30, 0,
-10, 20, 30, 20, 30, 20, -10,
-30, -10, 0, 30, 0, -10, -30
]
Similarly, for the Head Scientist piece, we can utilise the following piece square table to encourage the AI to prevent the Head Scientist piece from approaching the edge of the board:
piece_square_table_headscientist = [
10000, 10000, 10000, 10000, 10000, 10000, 10000,
10000, 1000, 1000, 1000, 1000, 1000, 10000,
10000, 1000, 0, 0, 0, 1000, 10000,
10000, 1000, 0, 0, 0, 1000, 10000,
10000, 1000, 0, 0, 0, 1000, 10000,
10000, 1000, 1000, 1000, 1000, 1000, 10000,
10000, 10000, 10000, 10000, 10000, 10000, 10000
]
Note that this is a very subjective part of the engine. Even in chess engine development, the Piece-Square Tables are very subjective and different developers tweak there tables to make their chess engines play with different styles.
With tafl being a niche strategy game, the history of engine development for the game is not well-documented. As a result I could not find any documentation on piece square tables for the game of tafl and in turn I deduced my own piece square tables based on a trial and error approach.
That said, with material balance and piece positioning accounted for, a simplified version of the evaluation function looks akin to the following:
function _evaluate_board()
local score=0
for square in all(board_squares) do
if square == 0 then
-- empty square --> pass
elseif piece[square] == infected then
score -= (value_infected + piece_square_table_infected[square])
elseif pieces[square] == scientist then
score += (value_scientist + piece_square_table_scientist[square])
else
score += (value_headscientist + piece_square_table_headscientist[square])
end
end
if side == scientists then
return score
else
return -score
end
end
Optimising Performance
At this stage we now have a working AI that plays at a passable level! However, to play at a passable level it takes far too long to evaluate all possible moves in a given position. This is a common issue for this type of game, as the number of potential moves increases exponentially with each turn. To tackle this issue, I implemented a couple of techniques to optimise the AI's performance and make it faster without compromising its ability.
These optimisation techniques are alpha-beta pruning and move ordering.
Alpha-Beta Pruning
Alpha-beta pruning is a technique used to reduce the number of nodes evaluated in the Minimax algorithm. By keeping track of the best score that the maximising and minimising players can achieve at any point in the search, we can eliminate branches of the game tree that will not influence the final decision. Effectively, this allows the engine to realise when it's researching a bad move and therefore can stop wasting time analysing the variation any further. This drastically reduces the time needed for the AI to make decisions, particularly in complex board states.
It helps to run through the alpha-beta pruning algorithm with an example; I found the following video by Sebastian Lague to be an excellent resource when attempting to wrap my head around how exactly this algorithm works in practice.
Hopefully we can now see how alpha-beta pruning is an efficient way to search through a decision tree, skipping branches that cannot influence the final outcome. However, the order in which we evaluate moves plays a crucial role in determining how much time we actually save.
If we evaluate the best move first, the algorithm quickly identifies strong bounds (alpha and beta values). This allows us to prune more branches early. However, if the best move is evaluated last, we explore many unnecessary branches before pruning, and the efficiency of the algorithm diminishes.
To address this, we can implement move ordering. This is a method to prioritise searching the most promising moves early in the search; this way we increase the likelihood of pruning irrelevant branches sooner.
Move Ordering
In order to effectively order the legal moves so that the most promising moves are evaluated first we can use the following optimisation techniques together; iterative deepening coupled with a principal variation search.
While it may sound intimidating with a name like "Iterative deepening", it is a surprisingly simple technique to implement; the AI starts by searching the game tree to a shallow depth first and then progressively deepens the search.
While this might seem counterintuitive, when coupled with a move ordering algorithm (such as a principal variation search) it allows the engine to prioritise exploring the most promising moves early on, which often results in better pruning and faster performance overall.
Lets look at how the principal variation search works with an example:
- Starting with Depth 1: The engine begins by searching 1 move ahead (depth 1) to find the optimal move at this level.
- Re-examining at Depth 2: When the engine expands the search to depth 2, it examines the previously identified optimal move first. While this move may not turn out to be the best at depth 2, it is likely to be a strong candidate and provides a good starting point for further exploration.
By starting with a strong candidate, the algorithm can quickly establish tighter bounds for alpha (score maximiser) and beta (score minimised) values, allowing it to prune less promising branches of the decision tree earlier and more effectively.
Conclusions and Future Development
Building an AI that can play tafl effectively in Pico-8 was a challenging but incredibly rewarding experience. Writing a chess engine from scratch and adapting it to play tafl required a deep dive into game AI, optimisation techniques, and creative problem-solving within Pico-8’s constraints.
While the AI isn't perfect, it plays a pretty decent game and seems to provide an engaging challenge for players! However, there is still much more room for improvement.
From initial player feedback, one area for future improvement is to add an Opening Book. Currently, the AI in Ziege will always react in the same manner to a series of opening moves, meaning that if you can remember how you've beaten the AI before, you can always beat it again by playing that same series of moves. The addition of an Opening Book would help address this by enabling the AI to vary its moves during the opening phase, making each game feel less predictable and more challenging.
If you have stuck with me this far, thank you for reading! I hope by sharing my process this will have provided some insight for anyone else looking to build a similar chess-like AI opponent for their strategy games. I’ve learned a lot from the experience, and while my approach isn’t definitive, I think it could be useful for others facing similar challenges.
Get Ziege
Ziege
An abstract turn-based strategy game. Outsmart the horde in a battle of wits.
| Status | Released |
| Author | Ross McCormick |
| Genre | Strategy |
| Tags | 8-Bit, Board Game, chiptune, Cute, PICO-8, Pixel Art, Singleplayer, tafl, Turn-based Strategy, Zombies |

Leave a comment
Log in with itch.io to leave a comment.